Kryptografia asymetryczna

Kryptografia krzywych eliptycznych (ang. elliptic curve cryptography – ECC) to jedna z kilku technik szyfrowania asymetrycznego z wykorzystaniem kluczy publicznych.

Technika ta jest szeroko wykorzystywana w szyfrowaniu danych, podpisach cyfrowych, generowaniu liczb pseudolosowych, czy w sieciach blockchain. Bitcoin wykorzystuje algorytm ECDSA do podpisywania transakcji w sieci używając klucza publicznego jako adresu portfela, eliminując konieczność jego propagacji.

Zapisz się do Blockchain Prasówki!

Newsy. Prasówka. Zamknięta grupa. Wchodzisz w to?

*Zapisując się wyrażasz zgodę na przesłanie Ci komunikacji marketingowej
pocztą elektroniczną. Przeczytaj Politykę Prywatności.

Leave this field empty if you’re human:

Nawet teraz czytając ten wpis, korzystasz z kryptografii asymetrycznej, która zapewnia bezpieczną komunikację między Twoją przeglądarką, a naszym serwerem. Klikając kłódeczkę w przeglądarce internetowej obok adresu strony https://chainkraft.com znajdziesz informacje na temat certyfikatu SSL.

Szyfrowanie symetryczne

Zanim przejdziemy do właściwego opisu ECC omówimy dwie główne kategorie algorytmów szyfrujących.

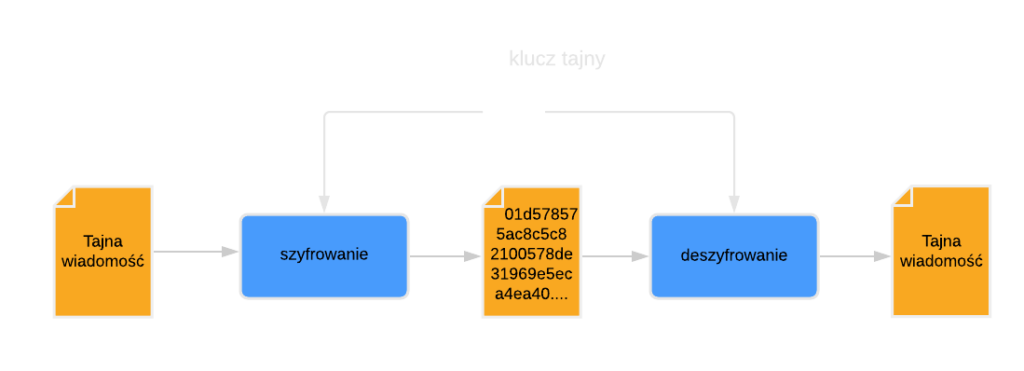
Szyfrowanie symetryczne wykorzystuje do działania tylko jeden klucz, tzw. klucz tajny. Klucz ten jest wykorzystywany zarówno przez nadawcę, który szyfruje wiadomość, jak i przez odbiorcę, który ją deszyfruje. Aby umożliwić bezpieczną komunikację pomiędzy stronami, klucz musi zostać przekazany odbiorcy wiadomości w bezpieczny sposób. W przypadku przechwycenia klucza przez osobę trzecią, może ona odszyfrować lub zmodyfikować treść wiadomości i przesłać ją do odbiorcy.

Szyfrowanie asymetryczne

Kryptografia asymetryczna wykorzystuje parę matematycznie powiązanych ze sobą kluczy – klucza publicznego oraz klucza prywatnego. Jeden klucz służy do szyfrowania, natomiast drugi do deszyfrowania wiadomości.

Klucz publiczny udostępniany jest każdej osobie która chce zaszyfrować wiadomość. Deszyfrowanie wiadomości możliwe jest wyłącznie z wykorzystaniem klucza prywatnego, który powinien być pilnie strzeżony.

Obliczenie klucza prywatnego na podstawie klucza publicznego powinno być matematycznie trudne. W przeciwnym razie opublikowany klucz publiczny pozwalałby na łatwe uzyskanie klucza prywatnego, a co za tym idzie deszyfrowanie wiadomości.

Trapdoor function

Ang. Trapdoor function (funkcja jednokierunkowa, zapadkowa) to funkcje matematyczne, które są łatwe do obliczenia, ale tylko w jednym kierunku. Obliczenie odwrotności funkcji, powinno być bardzo trudne, uniemożliwiając zakończenie obliczeń w rozsądnym czasie bez dodatkowej informacji.

Poniżej prezentujemy przykład funkcji która nie jest funkcją jednokierunkową:

A = B + C

Znając B oraz C bardzo łatwo obliczyć A. Obliczenie wartości C jeśli znamy A oraz B również nie stanowi problemu:

C = A - B

Z kolei przykładem funkcji jednokierunkowej jest faktoryzacja iloczynu, czyli jego rozkład na czynniki pierwsze – mnożną i mnożnik.

A = B * C
A = 1409 * 1823 = 2568607

Bardzo szybko jesteśmy w stanie obliczyć wynik mnożenia dwóch liczb pierwszych 1409 oraz 1823, który wynosi 2568607. Jeśli jednak odwrócimy tą operację i mając liczbę 2568607spróbujemy obliczyć czynniki z których powstała (faktoryzacja) to zajmie nam to nieporównywalnie więcej czasu. Przykładowe liczby są bardzo małe i raczej nie byłoby problemem obliczenie czynników metodą brute force w krótkim czasie. Jednak obliczenie czynników pierwszych liczb wykorzystywanych we współczesnych algorytmach kryptograficznych może zająć klika tysięcy lat! Czas obliczania faktoryzacji rośnie wykładniczo wraz ze wzrostem długości rozkładanej liczby.

Obecne algorytmy kryptograficzne wykorzystują liczby pierwsze składające się z kilkuset cyfr, aby można było uważać je za bezpieczne.

RSA

Na problemie faktoryzacji liczb całkowitych oparty jest najpopularniejszy obecnie algorytm kryptografii asymetrycznej – RSA.

Przykład działania algorytmu RSA.

1. Wybieramy dwie liczby pierwsze
p = 7 i q = 19

2. Obliczamy n = p * q
n = 7 * 19 = 133

3. Obliczamy funkcję Eulera φ(n) = (p - 1) * (q - 1) 
φ(n) = (7 - 1) * (19 - 1) = 6 * 18 = 108

4. Wybieramy liczbę e taką, że 1 < e < φ(n). Liczba e oraz φ(n) muszą być względnie pierwsze.
Niech e = 29

Nasz klucz publiczny: (e, n) => (29, 133)

5. Obliczamy multiplikatywną odwrotność e % φ(n). (więcej info - http://informatyka.wroc.pl/node/442?page=0,1)
Prostym językiem - obliczamy równanie: (d * e) % φ(n) = 1
(d * 29) % 108 = 1
d = 41 (kalkulator - https://www.dcode.fr/modular-inverse)

Nasz klucz prywatny: (d, n) => (41, 133)

Dlaczego algorytm dla wartości p = 3 i q = 7 nie ma sensu?

Zadanie domowe

Wiemy jak obliczać klucze asymetryczne w algorytmie RSA, ale jak szyfrować oraz deszyfrować wiadomości za ich pomocą?

Przykład uproszczonego szyfrowania oraz deszyfrowania wiadomości o treści H (od Hello) algorytmem RSA.

0. Dane
Klucz publiczny: (e, n) => (29, 133)
Klucz prywatny: (d, n) => (41, 133)
Wiadomość: H

1. Konwertujemy literę H na liczbę, przyjmując alfabetyczną kolejność
m = 8

2. Szyfrujemy dane kluczem publicznym obliczając c = m^e % n
c = 8^29 % 133 = 50
Zaszyfrowana wiadomość: 50

3. Deszyfrujemy dane kluczem prywatnym obliczając t = c^d % n
t = 50^41 % 133 = 8
Deszyfrowana wiadomość: 8
Po konwersji cyfry na odpowiednią literę alfabetu otrzymujemy: H

Konieczność obliczenia równania matematycznego t = c<sup>d</sup> % n zawierającego zmienną d z klucza prywatnego, uniemożliwia deszyfrowanie wiadomości za pomocą klucza publicznego. Powyższe kroki algorytmu RSA zostały bardzo mocno uproszczone, aby zaprezentować w przystępny sposób jego wysokopoziomowe działanie.

Warto zauważyć, że zmienna e oraz n wchodzące w skład klucza publicznego są „ogólnodostępne”. Znając faktoryzację liczby całkowitej n (brakujące ogniwo), jesteśmy w stanie obliczyć d, a co za tym idzie złamać szyfrowanie.

Aby uważać algorytm RSA za bezpieczny, należy wybierać coraz większe liczby pierwsze. Przykładowo algorytm RSA-2048 wykorzystuje liczby składającą się z 617 cyfr, które finalnie wpływają na wielkość generowanych kluczy. Na dzień dzisiejszy największym kluczem RSA jaki oficjalnie udało się rozbić na czynniki pierwsze jest klucz 768 bitowy w ramach konkursu RSA Factoring Challenge.

Elliptic curve cryptography

Kryptografia krzywych eliptycznych wykorzystuje inną funkcję jednokierunkową (ang. trapdoor function) do generowania kluczy asymetrycznych. Algorytm RSA zawdzięcza bezpieczeństwo problemowi faktoryzacji liczb całkowitych na czynniki pierwsze. Natomiast ECC bazuje na problemie logarytmu dyskretnego zakładając, że znalezienie losowego punktu na krzywej eliptycznej na podstawie punktu bazowego, jest praktycznie niewykonalne dla współczesnych komputerów.

Krzywe eliptyczne to obiekty których punkty spełniające konkretne równanie matematyczne: y<sup>2</sup> = x<sup>3</sup> + ax + b. Na początek naszej matematycznej przygody, dla ułatwienia osadzimy nasze współrzędne w zbiorze liczb rzeczywistych x, y ∈ R.

Krzywe eliptyczne tworzą matematyczną grupę, które charakteryzują się pewnymi właściwościami. Punkty możemy dodawać, istnieje element neutralny, a każdy element, posiada element przeciwny.

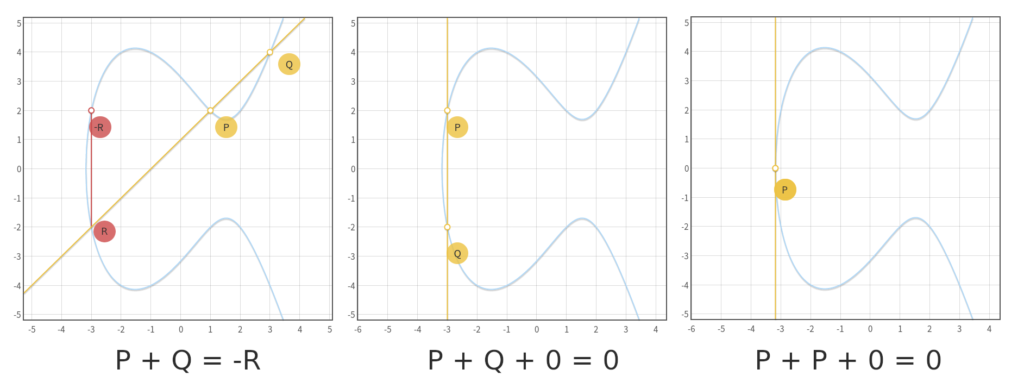
Dla nas najbardziej interesującą właściwością (P + Q + R = 0) jest dodawanie trzech punktów leżących na krzywej, których suma zawsze wynosi 0 (element neutralny).

Dodawanie trzech punktów w krzywej eliptycznej:

1. Na początku rysujemy prostą, która przechodzi przez punkty P i Q.
2. Narysowana prosta powinna przeciąć krzywą co najwyżej w trzecim miejscu, który oznaczamy jako punkt R.
3. Ostatecznym wynikiem dodawania, będzie odbicie punktu R względem osi X.

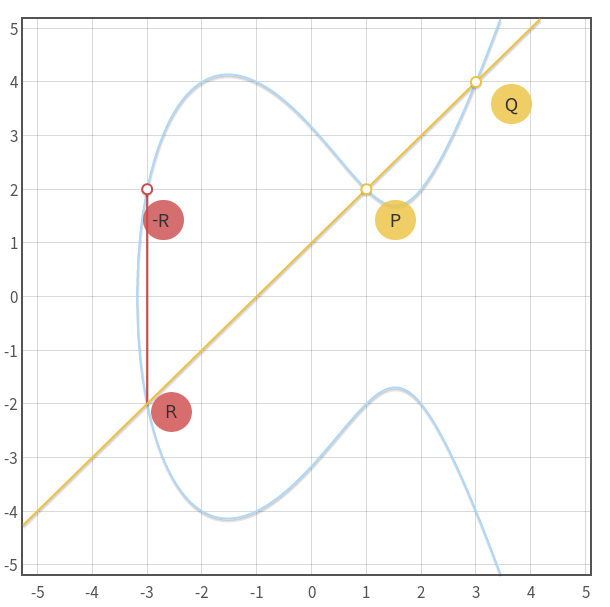
Dzięki tej właściwości, mając dwa punkty na krzywej eliptycznej, możemy obliczyć trzeci punkt, który jest ich sumą. Późniejszym krokiem będzie wykorzystanie tej zależności do stworzenia jednokierunkowej funkcji.

Powyższe piękne rysunki dotyczą krzywych eliptycznych w przestrzeni liczb rzeczywistych. W kryptograficznych zastosowaniach krzywe eliptyczne osadzone są w przestrzeni liczb skończonych wykorzystując do tego celu arytmetykę modulo p (obliczamy reszty z dzielenia), gdzie p to bardzo duża liczba pierwsza.

Przykładowy skończony zbiór liczb całkowitych modulo 5, będzie posiadał 5 elementów, ponieważ tyle różnych reszt z dzielenia przez 5 możemy uzyskać.

0 % 5 = 0
1 % 5 = 1
2 % 5 = 2
3 % 5 = 3
4 % 5 = 4
5 % 5 = 0
6 % 5 = 1
7 % 5 = 2
8 % 5 = 3
[...]
F5 = {0, 1, 2, 3, 4}
Fp = {0, 1, 2, ..., p - 1}

Równanie krzywej eliptycznej w zbiorze liczb całkowitych skończonych modulo p będzie miało lekko zmodyfikowaną postać: y<sup>2</sup> = x<sup>3</sup> + ax + b (mod p)

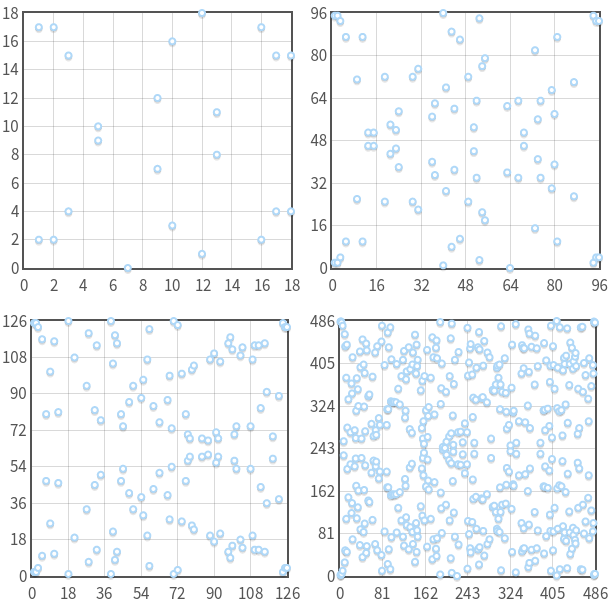
Krzywe eliptyczne otrzymane z tego równania, wyglądają jak losowo rozrzucone punkty po układzie współrzędnym. Nie mniej jednak wszystkie właściwości, które zostały omówione wcześniej, są zachowane. Możemy nawet zauważyć symetrię punktów względem osi X.

Dla przećwiczenia opisanego konceptu odsyłamy do przydatnego narzędzia do rysowania krzywych eliptycznych w arytmetyce modulo: https://www.graui.de/code/elliptic2/

Operacje matematyczne na krzywych eliptycznych w zbiorze liczb skończonych całkowitych będą miały takie same właściwości jak na zbiorze liczb rzeczywistych, dzięki wykorzystaniu liczby pierwszej w operacjach modulo. Poniżej prezentujemy interaktywny przykład dodawania trzech punktów na krzywej eliptycznej w skończonym zbiorze liczb całkowitych modulo 97.

Skoro wiemy już jak dodawać punkty na krzywej eliptycznej, zróbmy teraz kolejny krok i poznajmy kluczową operację wykorzystywaną na potrzeby kryptografii tzw. podwajanie punktu (ang. point doubling).

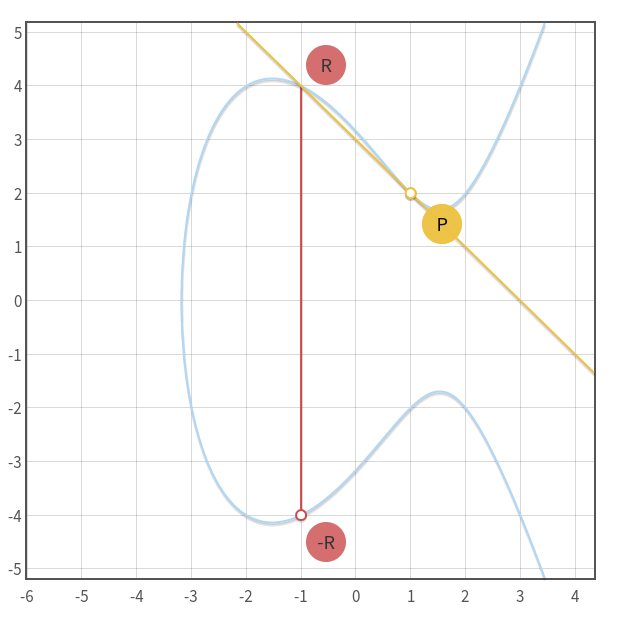
Dodawanie dwóch różnych punktów definiujemy wzorem P + Q = -R. Ale czy możemy dodać do siebie ten sam punkt? Jak najbardziej! Otrzymamy wtedy równanie P + P = -R lub 2P = -R.

Wykorzystując poznane operacje dodawania oraz podwajania punktu możemy wprowadzić operację mnożenia punktów na krzywej eliptycznej:

Podwajanie punktu:
P + P = -R
2P = -R

Mnożenie punktu:
xP = -R

Przykładowe mnożenie punktu za pomocą operacji dodawania i podwajania:
7P = -R
1P + 6P = -R
1P + 2P + 2P +2P = -R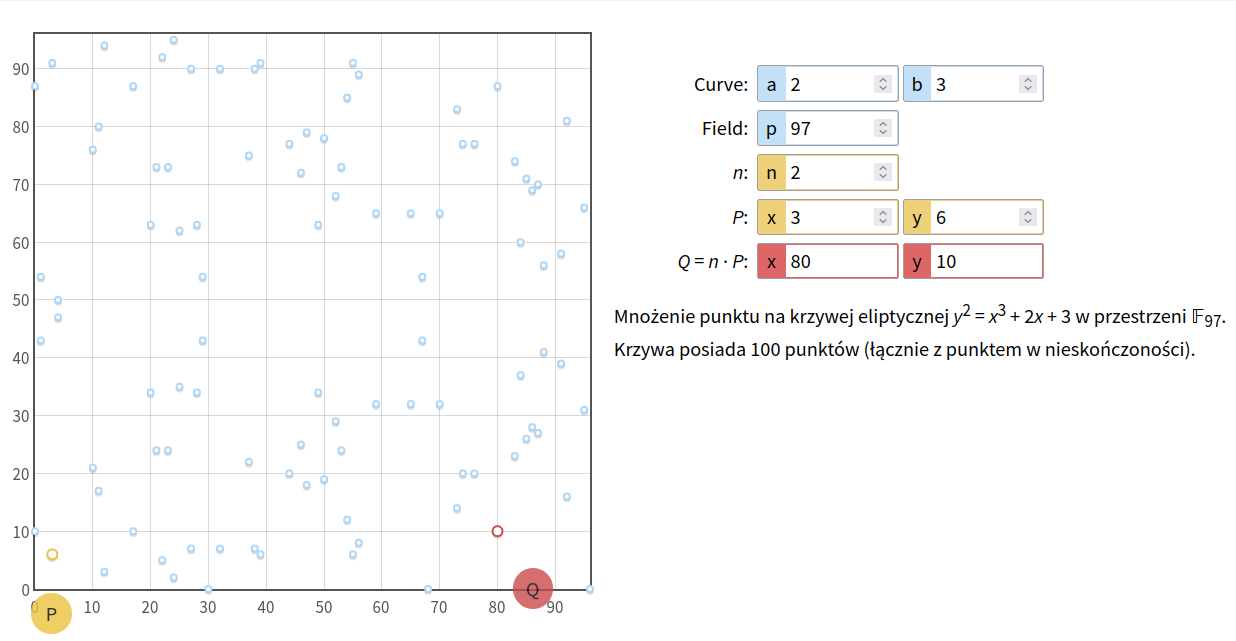

Dotarliśmy to miejsca, gdzie jesteśmy w stanie zdefiniować jednokierunkową funkcję (ang. trapdoor function) opartą na arytmetyce krzywych eliptycznych:

xP = Q

Tak, jest to po prostu obliczanie wielokrotności naszego punktu, które właśnie poznaliśmy. Bardzo łatwo obliczyć wielokrotność punktu Q, mając współrzędne P oraz mnożną x. Natomiast niemożliwym jest obliczenie mnożnika x mając do dyspozycji P oraz Q w rozsądnym czasie. Jest to tzw. problem logarytmu dyskretnego dla krzywych eliptycznych (ang. Elliptic Curve Discrete Logarithm Problem).

Funkcja jednokierunkowa:
xP = Q

Klucze asymetryczne:
Q - klucz publiczny
x - klucz prywatny
P - punkt początkowy (parametr)
klucz publiczny = klucz prywatny * punkt początkowy

W przypadku kryptografii asymetrycznej, punkt początkowy P leżący na krzywej jest z góry zdefiniowanym parametrem wejściowym. Kluczem prywatnym jest parametr x, czyli nasza mnożna (liczba całkowita). Natomiast wynik operacji Q – wielokrotność punktu początkowego, to nasz klucz publiczny.

Jedyną metodą na złamanie klucza prywatnego x jest obliczanie kolejnych wielokrotności punktu P, aż do osiągnięcia wielokrotności w punkcie Q. Brzmi prosto, ale zastosowanie wielkich liczb dla P oraz x praktycznie uniemożliwia obliczenie tego w rozsądnym czasie.

RSA vs ECC

Zastosowanie matematycznych krzywych eliptycznych w kryptografii pozwoliło na znaczne zredukowanie wielkości generowanych kluczy, przy jednoczesnym zachowaniu poziomu bezpieczeństwa. Dzięki temu algorytmy ECC są szybsze oraz konsumują mniej zasobów generując klucze.

Poniżej prezentujemy porównanie rozmiarów kluczy (ilość bitów) dla różnych metod kryptograficznych z zachowaniem poziomu bezpieczeństwa.

Klucze symetryczne	Klucze RSA	Klucze ECC
80	1024	160
112	2048	224
128	3072	256
192	7680	384
256	15360	521

Ciągły rozwój mocy obliczeniowych komputerów sprawia, że wielkość kluczy asymetrycznych musi być zwiększana, aby zachować bezpieczeństwo. Na dzień dzisiejszy instytucja NIST rekomenduje używanie 2048 bitowych kluczy RSA (do roku 2030). Wykorzystując algorytmy ECC z analogicznym poziomem bezpieczeństwa redukujemy rozmiar kluczy o około 90%!