Hashing generates a fixed-length string (the “hash” or “message digest”) from an input (the “message”) of arbitrary length. While hashing outputs a seemingly random string, a given message will always produce the same digest. Even the smallest change of input data will result in a completely different hash.
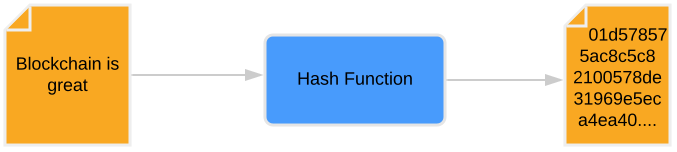
Hashing is an irreversible process as it is virtually impossible to recreate the original message from the hash. Different hash functions generate hashes of varying lengths. For example, the popular SHA256 function produces a 256-bit hash, while MD5, a function now considered insecure, outputs a 128-bit hash.
MD5(chainkraft) = 428aa4bbd0dae9b27050f89492008ee2
SHA1(chainkraft) = 2ad43800879e33005089df2fbea6de0160e08f73
SHA256(chainkraft) = 95bc529ef76da85bb79d106aeef096d1b4c8fd93d67340f6d07bb8b01952a356
Keccak512(chainkraft) = 0bb2141d86ce67125303897970e409d08d25ff170104b87a3dcba5678610a93603f7227d325f48a6a982d709bf74e822606c1da88074e6a455104a9fa7a86b7aApplications
Thanks to their properties, hash functions are used in a wide range of applications. Below are just a few examples of their practical implementations.
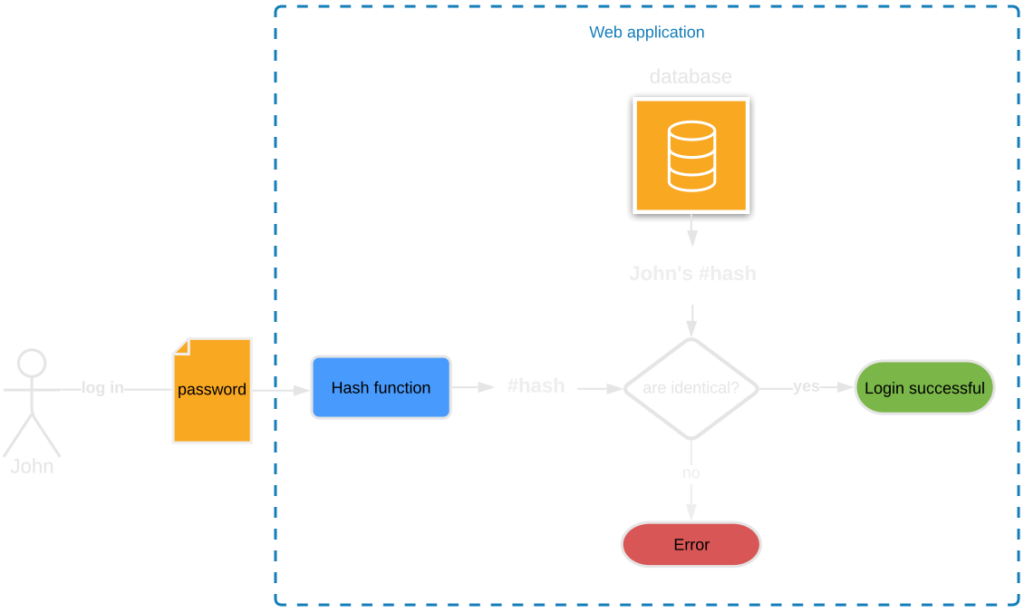
Password storage
Thanks to the one-way property of hash functions, they are used for storing passwords in IT systems, with virtually every website offering user account functionality storing user passwords as hashes. Passwords stored in plain text would be easy pickings for hackers if the website was compromised. Users using one password for multiple websites would be particularly at risk as one stolen password would grant access to several accounts.
During the account registration process, users define their passwords which are then hashed and saved in a database. When signing in, the password input in the signup form is hashed and then compared against the digests stored in the database (remember? the same input will always generate the same hash).
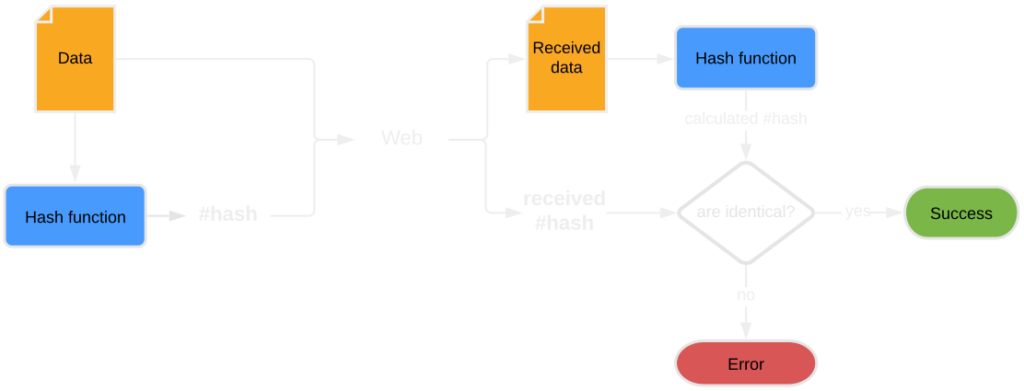
Data integrity
Hashing functions are most widely used for data integrity control. The function generates a hash based on the input (e.g. a photo file), which becomes the so-called checksum, a data fingerprint of sorts. Even the slightest modification in the data structure will result in a different checksum being generated, which facilitates the effective verification of the integrity of data sent over the Internet by the recipient.
Blockchain
Without cryptographic hash functions, an efficient and secure blockchain network would be almost impossible to create. Bitcoin and many other blockchains use Proof-of-Work as a consensus mechanism to ensure network security. Hashing is a basic operation of the Proof-of-Work method whose purpose is to “mine” a new block of confirmed transactions.
Hashes also have other applications in blockchains as they are used to generate addresses and facilitate quick transaction verification using Merkle trees.
Properties
Let’s review some properties of hash functions and learn about the properties of their special subgroup, namely cryptographic hash functions.
Fixed-length hash
No matter the size of the input, be it 1KB of data or a 2 GB file, the output hash should always be of fixed length as the hash length depends on the hash function used, not the length of the message.
| Hash function name | Hash length [bits] |
|---|---|
| SHA-1 | 160 |
| SHA-256 | 256 |
| SHA-512 | 512 |
| RIPEMD-320 | 320 |
| Whirlpool | 512 |
Deterministic
A hash generated from a given input should always be identical.
hash1(test) = hash2(test) … = hashn(test)However, even the slightest change in input data should generate a completely different, uncorrelated hash (avalanche effect). Example:
hash(test) = 098f6bcd4621d373cade4e832627b4f6
hash(Test) = 0cbc6611f5540bd0809a388dc95a615bEfficiency
Hash functions should be efficient and fast to compute. Regardless of the input size, the result should be returned very quickly to render the algorithm applicable in practice.
Pre-image resistance
This property denotes that hash computation by hash functions is unidirectional, meaning that generating a hash from the input is a one-way operation. Given hash(x), it should be impossible to determine input x on its basis.

Second pre-image resistance
Given inputs x, it should be virtually impossible to find such inputs y for which the computed hash would be the same: hash(x) ! = hash(y). This property is also referred to as weak collision resistance.
Collision resistance
Collision resistance is a property whereby it is extremely difficult to find two different inputs for a hash function that would return the same hash: hash(x) ! = hash(y).
On account of their nature, hash functions will always generate some collisions. After all, there is an infinite number of different types (and lengths) of inputs and hashes have a certain maximum length; hence the number of potential combinations is limited. The idea is to make such collisions near impossible to find.
Algorithm concept
Below is a high-level description of how a typical hash function works. We won’t go into details as they can vary significantly from algorithm to algorithm.
How come hash functions generate a fixed-length hash from an input of arbitrary length, and that hash is the same with every function call? This follows from the basic concept underlying most hash functions whereby, for processing, inputs are divided into smaller blocks of equal length.
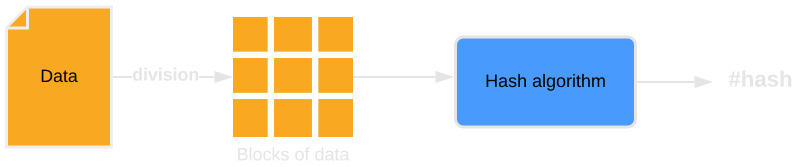
The size of the data block varies depending on the algorithm. For example, the SHA-256 function uses 512-bit blocks. Typically, the size of the input is not a multiple of the block size. In such cases, padding is applied. Padding consists in adding data to the final input block to match the length of the previous blocks and the block size of the given function.
After dividing the message into fixed-length blocks, the sequential process of hash computation can be started. This process involves running the hashing algorithm on each of the blocks.
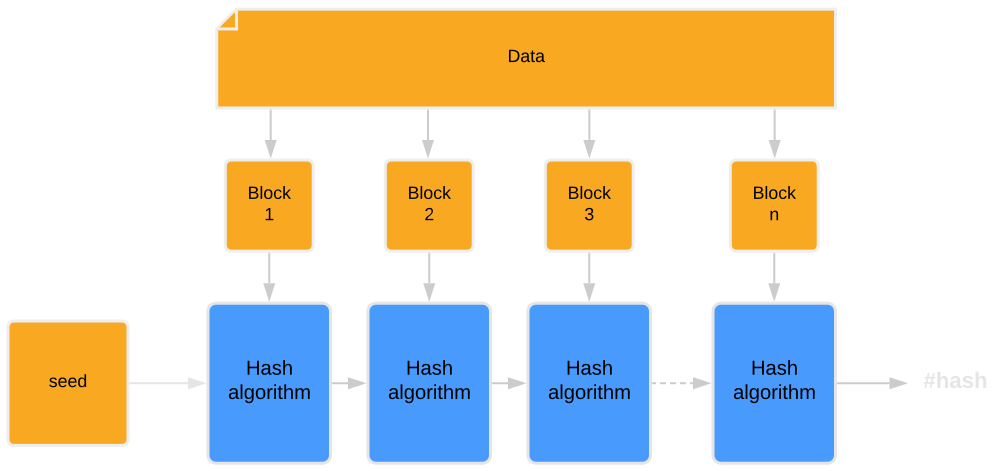
The function takes as parameters the data of the current block and the hash of the previous block. For example, when calculating the first block, the function takes data from Block 1 and the initialization values. Calculating the second block requires Block 2 data and the response from the function called on Block 1. The computation is repeated until the data computed from the last block return the final hash.
In practice, blocks are counted over around a dozen rounds (e.g. SHA-256 uses 80 rounds), and the value of the last hash is additionally compressed. By linking the algorithm’s calculations to the responses from the previous blocks, changing even one bit of data will generate a completely different hash (avalanche effect).