What are Merkle trees?
A Merkle tree (also called a hash tree) is a structure that stores data hashes in the form of a tree allowing for quick integrity verification. It is extensively used in peer-to-peer communication for verification of data exchanged between two untrusted parties. What’s more, Merkle trees can be used to verify data sent by a third party before it is even received!
Some practical examples of their application include the Bitcoin and Ethereum networks, BitTorrent protocol and the GIT version control system.
The basic element that makes up Merkle trees is cryptographic hash functions. If you haven’t heard of them before, read our article on hashing first:
Structure
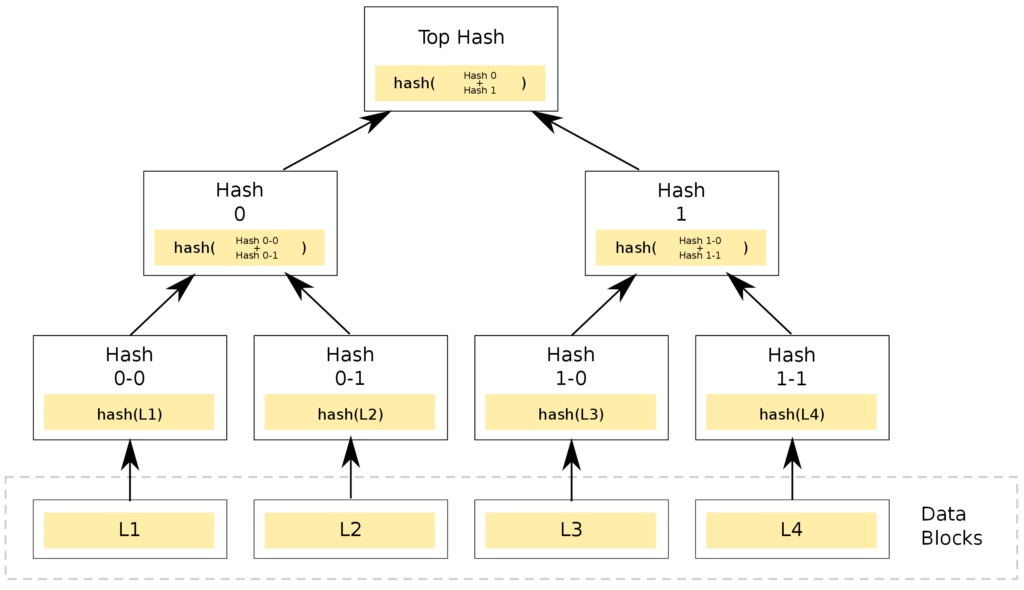
Rather than a regular tree, these structures are actually inverted trees. Their data structure goes from individual leaves with hashed data at the bottom, up to the root at the top. Please note that the lowest layer, “Data blocks”, is not part of the tree structure in the diagram above. In traditional file transfers, a large file is typically split into smaller data blocks downloaded in parallel by the client. This reduces the download time and allows for quicker reaction in the event of transfer errors or deliberate action.
Merkle tree example
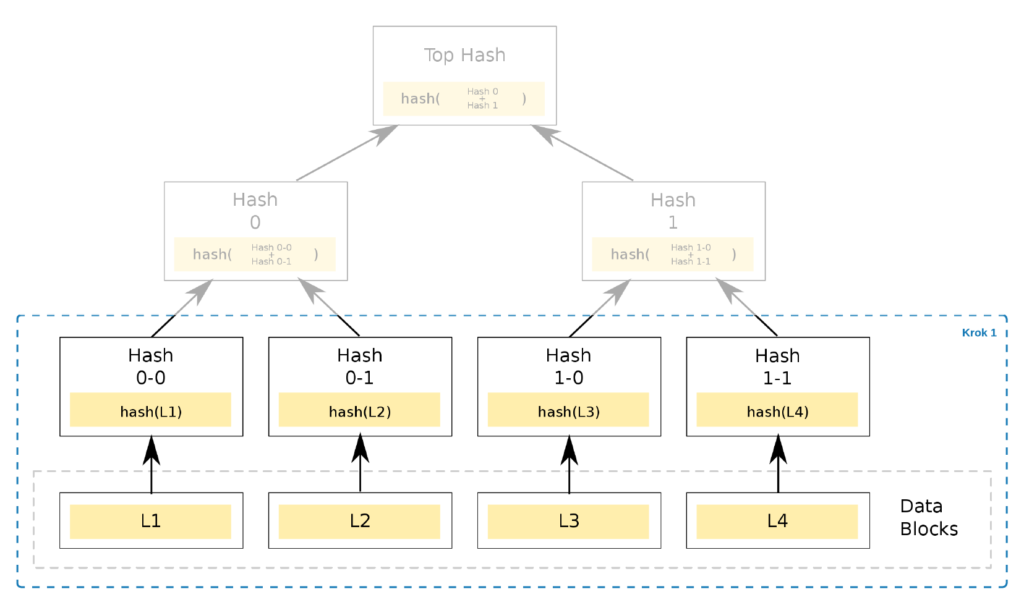
The first leaves in the tree are generated by computing the hash function (e.g. H(L1)) of each individual data block (L1, L2, L3, L4). Regardless of the data block size, the generated hash is of a fixed length (e.g. SHA256 will generate a 256-bit hash). The hash acts as a data signature. Any modification to the data will result in a completely different hash in the leaf being generated.
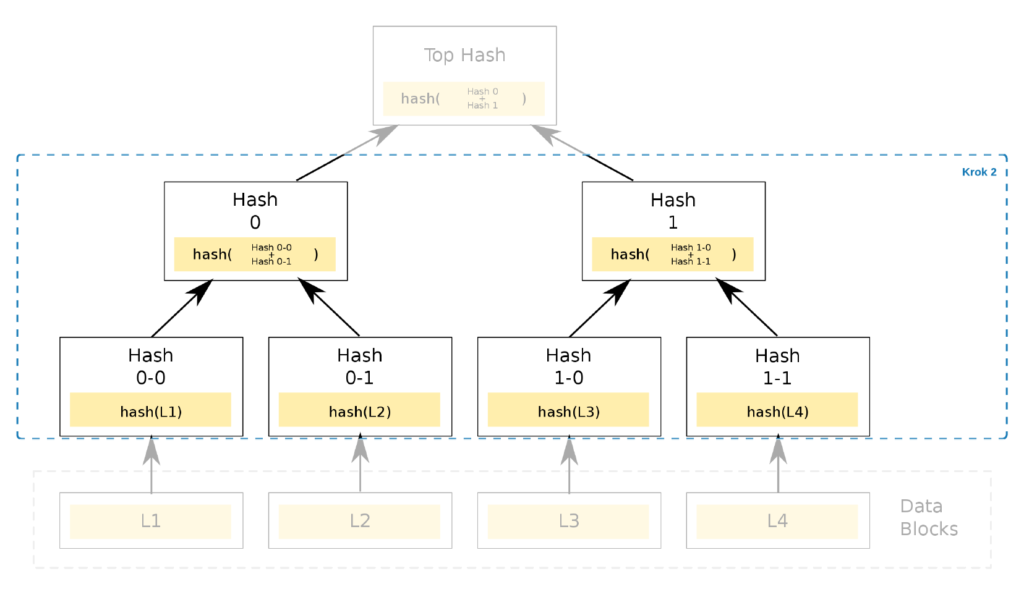
Merkle trees are typically binary trees, with each node having two children. Consecutive tree branches, all the way to the root at the top, are generated by hashing their children. The diagram shows that node S12 represents the hash of nodes S1 and S2: H(S1 || S2).
Up at the very top is the root of the tree, the Merkle root. The tree structure is sensitive to even the slightest change, as any modification to any data block will completely change the root hash!
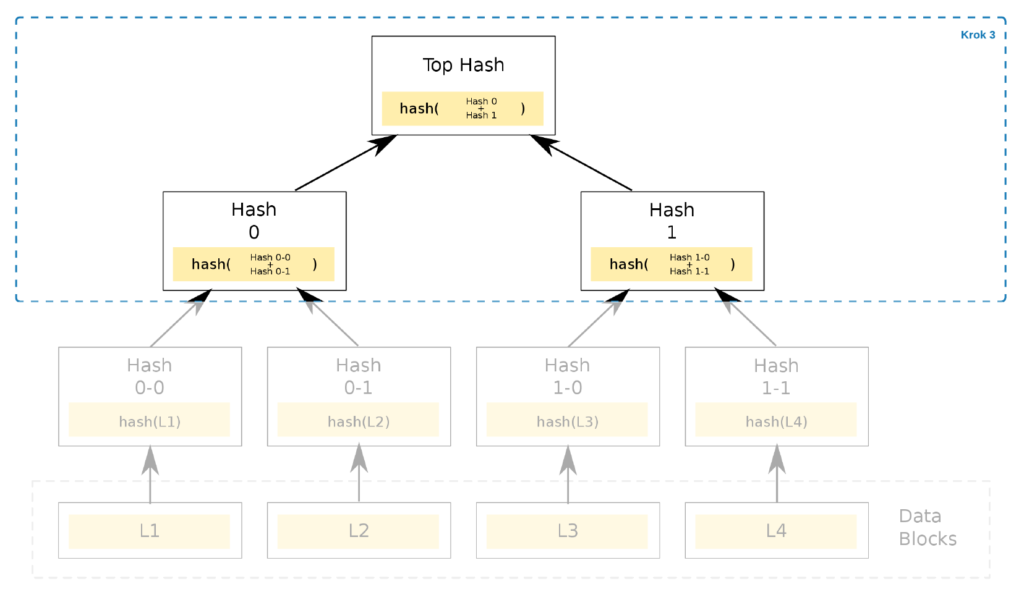
The root, usually obtained from an external trusted source, is sufficient to verify whether the file we want to download in a P2P network from an untrusted source is corrupt. It is a highly efficient solution as a mere 256-bit hash is enough to decide whether to start downloading a file from a specific source or not.
Application in blockchain
Just as an oak symbolizes stability, Merkle trees are the foundation of a stable blockchain network. Let’s review their practical application in the world’s most popular network, Bitcoin.
The primary purpose served by Merkle trees in blockchains is that of quick transaction verification. The tree is built based on transaction IDs grouped together in a block, with the computed tree root being saved in the block header.
As a reminder, blockchain networks, true to their name, store data blocks linked together to form a chain. Each data block contains grouped transactions, and each transaction has a unique ID.
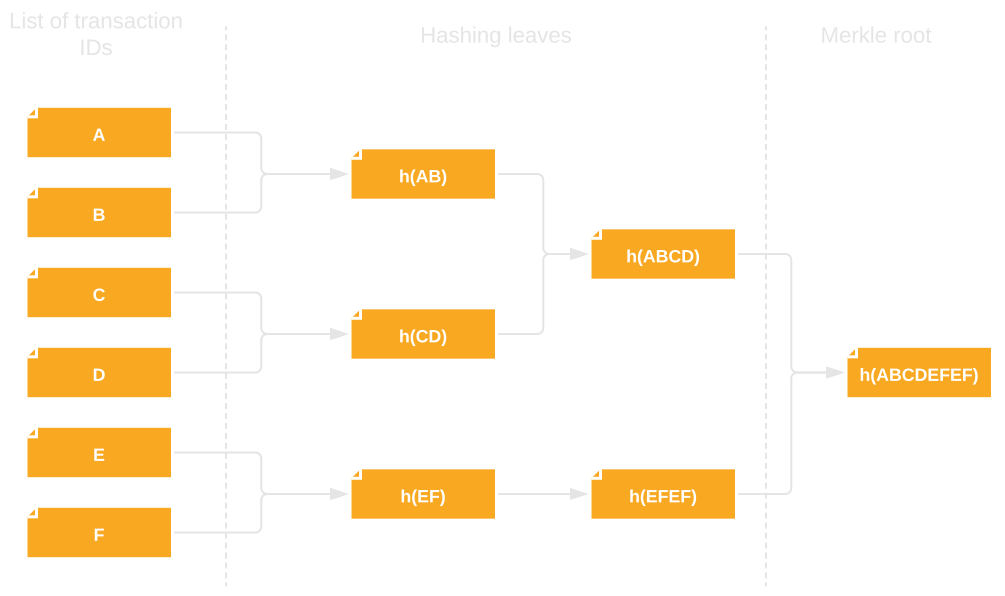
But why do we need Merkle trees to verify transactions at all? Without them, checking whether a specific transaction was included in a given block (and thus confirmed) would require downloading and running operations on large amounts of data. Remember – a single Bitcoin block can contain up to several thousand transactions! This data overhead and the need to compare individual records could prevent an efficient blockchain network from ever emerging.
Thanks to Merkle trees, the data validation process can be separated from the data itself. Thanks to this, transactions do not require a full copy of the blockchain (342 GB as at 04/04/2021) to be verified. This also enabled the introduction of Simplified Payment Verification (SPV) found in lightweight Bitcoin clients (Light Node – e.g. mobile phone wallets).
Example
Now let’s go through the steps of a sample validation to establish whether a transaction we made had already been included in a new block.
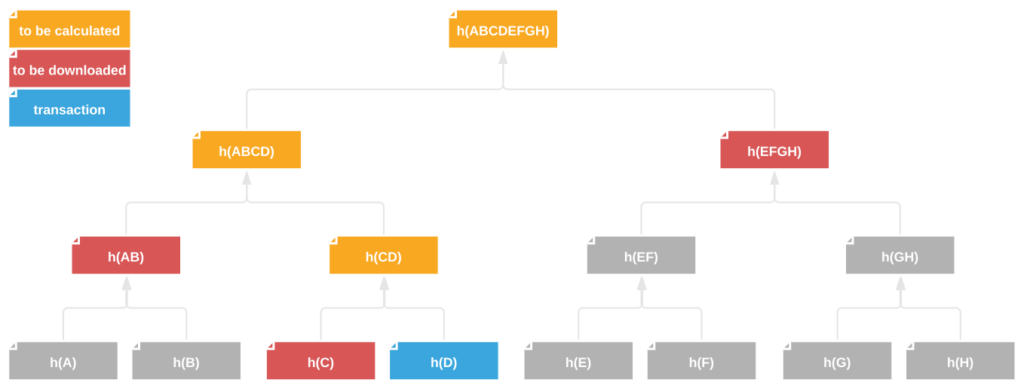
- The hash of our transaction ID is h(D).
- To compute the parent node h(CD), we have to take the transaction hash h(C).
- To calculate the next parent node, h(ABCD), we need to add hash h(AB).
- Finally, to obtain the tree root, we also need hash h(EFGH) representing the right-hand side of the tree.
The tree root obtained in step 4 is compared against the root in the header of a given block. If the hashes match, we can be certain that our transaction was included in the block. Employing the Merkle tree structure for data validation allowed us to reduce the amount of transferred data down to the required three hashes ((h(C), h(AB), h(ERGH)) and brought down the number of hash operations to three ((h(CD), h(ABCD), h(ABCDEFGH)). Missing data for verification is downloaded from network-connected clients storing the complete blockchain (e.g. miners). It is worth noting that the provided validation example is based on a Merkle tree built based on only eight transactions. A typical Bitcoin block holds up to several thousand transactions!
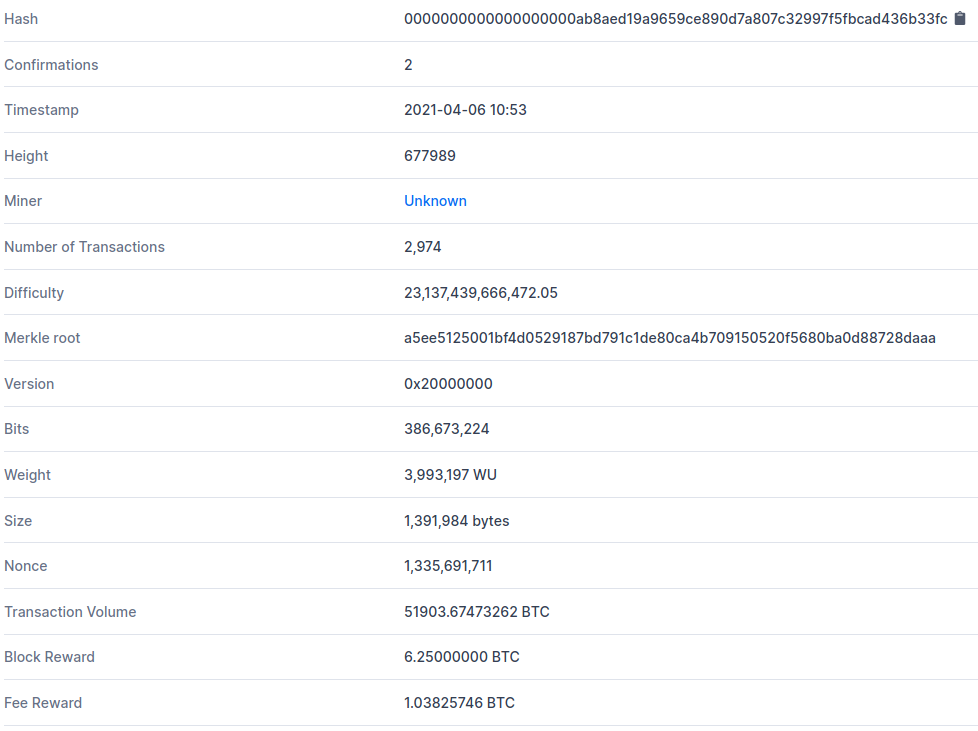
Example of the header of block 677989 containing the root of the Merkle tree calculated on the basis of 2,974 transactions:
Summary
Even though more than 40 years (1979) have passed since Ralph Merkle patented his data structure, Merkle trees are enjoying unwavering popularity. These structures facilitated the creation and meteoric rise of Bitcoin, the first complete cryptocurrency, ensuring efficient verification and integrity of transactions. At the time of writing this article, the data structure is responsible for the security of nearly $ 1.5 trillion in assets stored in the Bitcoin and Ethereum blockchains!



